Symbolic Artificial Intelligence
Section 1: Introduction
Symbolic Artificial Intelligence (Symbolic AI) is a foundational approach to AI that focuses on the manipulation of symbols and the application of logical rules to simulate intelligent behavior. Unlike statistical approaches such as machine learning and neural networks, Symbolic AI is deeply rooted in formal logic and aims to model human reasoning through structured representations and inference processes.
This paper provides a comprehensive introduction to Symbolic AI, covering its theoretical foundations, key methodologies, and applications. We begin by exploring the historical context and the early aspirations of AI researchers to replicate human intelligence through symbol manipulation. The paper then delves into the core concepts of Symbolic AI, including knowledge representation, inference engines, and the processes of symbol manipulation.
To illustrate these concepts, we present examples and diagrams that visualize the workings of Symbolic AI systems. We also contrast Symbolic AI with other AI paradigms, highlighting their fundamental differences and the unique strengths and limitations of Symbolic AI.
Furthermore, the paper explores the applications of Symbolic AI in various domains, such as expert systems, natural language processing, and automated reasoning. We discuss real-world use cases and case studies to demonstrate the practical impact of Symbolic AI.
Finally, we conclude by examining the future directions of Symbolic AI and its potential synergies with emerging approaches like neuro-symbolic AI. We discuss how the integration of Symbolic AI with other AI paradigms can lead to more robust and interpretable AI systems.
Throughout the paper, we strive to present the concepts in an accessible manner, using clear explanations and analogies to make the content engaging and understandable to readers with varying levels of expertise in AI.
Section 1: Historical Context
The roots of Symbolic Artificial Intelligence (AI) can be traced back to the early days of AI research in the 1950s and 1960s. During this period, a group of pioneering researchers, including John McCarthy, Marvin Minsky, Nathaniel Rochester, and Claude Shannon, laid the theoretical and philosophical foundations for the field of AI.
One of the seminal moments in the history of Symbolic AI was the Dartmouth Conference of 1956, organized by John McCarthy. This conference brought together leading researchers from various disciplines to discuss the possibility of creating intelligent machines. It was at this conference that the term “Artificial Intelligence” was coined by McCarthy, and the key ideas and goals of AI were articulated.

Following the Dartmouth Conference, several influential projects and programs were developed that shaped the course of Symbolic AI. One such project was the Logic Theorist, developed by Allen Newell, Herbert A. Simon, and Cliff Shaw in 1956. The Logic Theorist was one of the first programs designed to perform automated reasoning and prove mathematical theorems. It demonstrated the potential of using symbolic logic and heuristic search to solve complex problems.
Another significant development in the early days of Symbolic AI was the General Problem Solver (GPS) program, created by Newell and Simon in 1957. GPS was designed as a universal problem-solving engine that could tackle a wide range of problems by breaking them down into smaller subproblems and applying general problem-solving strategies. Although GPS had its limitations, it demonstrated the potential of using symbolic representations and heuristic search to solve complex problems.
Throughout the 1960s and 1970s, Symbolic AI continued to make significant strides. Researchers developed various knowledge representation formalisms, such as first-order logic, semantic networks, and frames, to capture and reason about domain knowledge. Expert systems, which aimed to emulate the decision-making abilities of human experts in specific domains, emerged as one of the most successful applications of Symbolic AI during this period.
However, in the 1980s and 1990s, Symbolic AI faced increasing challenges and criticisms. The brittleness of symbolic systems, the difficulty of scaling to real-world complexity, and the knowledge acquisition bottleneck became apparent. Critics, such as Hubert Dreyfus, argued that Symbolic AI was fundamentally limited in its ability to capture the full richness of human intelligence.
Despite these challenges, Symbolic AI has continued to evolve and find applications in various domains. The integration of symbolic and sub-symbolic approaches, as well as the emergence of neuro-symbolic AI, has opened up new possibilities for leveraging the strengths of both paradigms.
The historical context of Symbolic AI reveals a rich tapestry of ideas, achievements, and challenges. From its early beginnings at the Dartmouth Conference to its current state, Symbolic AI has played a crucial role in shaping our understanding of intelligence and pushing the boundaries of what machines can accomplish. As the field continues to evolve, the lessons learned from its history will undoubtedly inform and guide future research and development in AI.
Section 2: Theoretical Foundations
2.1 Formal Logic as the Backbone of Symbolic AI
Symbolic AI is fundamentally grounded in formal logic, which provides a rigorous framework for representing and manipulating knowledge. Formal logic allows for the precise specification of rules and relationships, enabling Symbolic AI systems to perform deductive reasoning and draw valid conclusions.
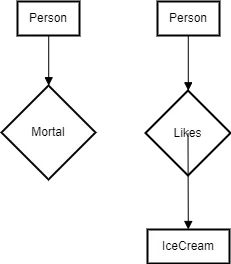
First-Order Logic (FOL) Examples
FOL is a powerful language for representing and reasoning about complex domains. It allows for the representation of objects, relations, and quantifiers. For example, consider the following FOL statements
| Statement | Meaning |
|---|---|
| Represents the idea that all persons are mortal. | |
| Asserts that there exists at least one person who likes ice cream. |
Diagram 1: First-Order Logic Representation
2.2 Search and Problem Solving
Search algorithms and problem-solving techniques are central to Symbolic AI. They enable systems to explore a space of possibilities and find solutions to complex problems.
Advanced Reasoning Techniques
Non-Monotonic Reasoning
Non-monotonic reasoning allows for the revision of conclusions in light of new information. It enables Symbolic AI systems to handle exceptions and make default assumptions. For example:
- Birds typically fly.
- Penguins are birds.
- Penguins do not fly.
In non-monotonic reasoning, the conclusion that all birds fly can be revised when the information about penguins is introduced.
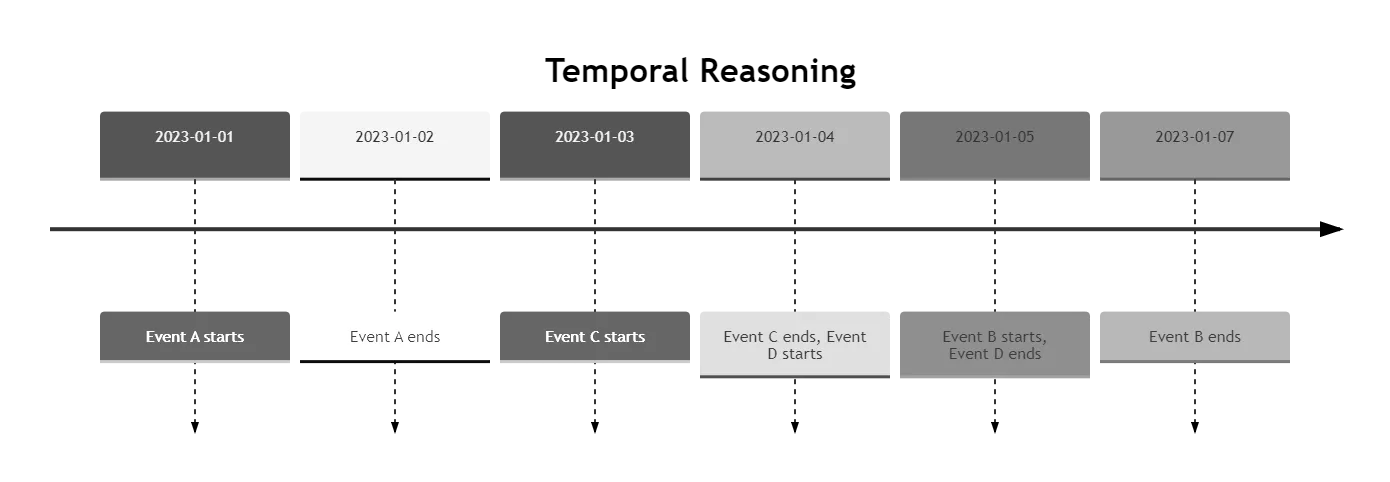
Temporal Reasoning
Temporal reasoning deals with the representation and reasoning about time-dependent knowledge. It involves reasoning about events, their durations, and temporal relationships. For instance:
- Event A occurs before Event B.
- Event B overlaps with Event C.
- Event D starts immediately after Event C ends.
Diagram 2: Temporal Reasoning
2.3 Knowledge Representation
Knowledge representation is a crucial aspect of Symbolic AI, as it determines how domain knowledge is structured and organized for efficient reasoning and problem-solving.
Semantic Networks
Semantic networks represent knowledge as a graph, where nodes represent concepts and edges represent relationships between concepts. For instance, consider the following semantic network:
Diagram 3: Semantic Network Representation
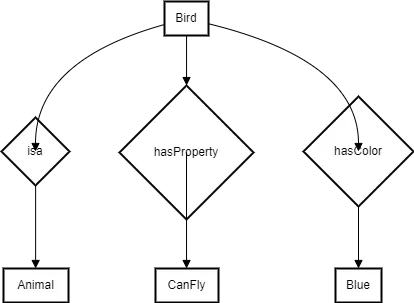
This semantic network represents the knowledge that a bird is an animal, birds can fly, and a specific bird has the color blue.
Frames
Frames are data structures that represent stereotypical situations or objects with slots for relevant properties and their values. Consider the following frame representation of a car:
Diagram 4: Frame Representation
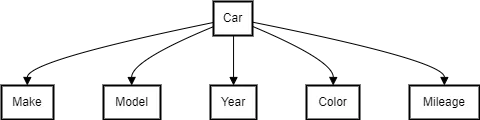
Each slot in the frame (e.g., Make, Model, Year) can be filled with specific values to represent a particular car instance.
2.4 Commonsense Reasoning
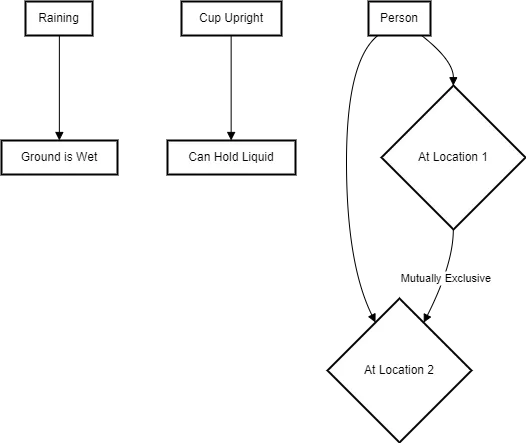
Commonsense reasoning involves the ability to make inferences based on everyday knowledge and understanding of the world. It encompasses reasoning about causality, spatial relationships, and general domain knowledge.
Example:
- If it is raining, the ground will be wet.
- A cup must be upright to hold liquid.
- A person cannot be in two different locations at the same time.
Diagram 5: Commonsense Reasoning
2.5 Symbol Manipulation and Representation
At the core of Symbolic AI lies the concept of symbol manipulation. Symbols are abstract representations of real-world entities, concepts, or relationships. These symbols are organized into structured representations, such as hierarchies, semantic networks, or frames, to capture the relationships and properties of the entities they represent.
2.5.1 Definition and Importance of Symbols in AI
Symbols in Symbolic AI are more than just labels; they carry meaning and enable the system to reason about the entities they represent. For example, in a medical diagnosis expert system, symbols like “fever,” “cough,” and “headache” represent specific symptoms, while symbols like “influenza” and “pneumonia” represent diseases. These symbols form the building blocks for expressing knowledge and performing logical inference.
2.5.2 Processes of Symbol Manipulation
Symbol manipulation in Symbolic AI involves three key processes:
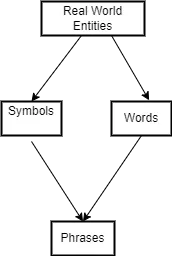
Creation and Definition of Symbols:
Symbols are created to represent the relevant entities, concepts, and relationships in a given domain. For example, in a natural language processing system, symbols may be created for words, phrases, and grammatical structures.
Diagram 6: Symbol Creation and Definition
Symbol Structuring
Once symbols are defined, they are organized into structured representations that capture the relationships and properties of the entities they represent. Common techniques for symbol structuring include semantic networks, frames, and ontologies.
Diagram 7: Symbol Structuring (Semantic Network)
Rule Application
Symbolic AI systems use predefined logical rules to manipulate symbols and derive new knowledge. These rules specify how symbols can be combined, transformed, or inferred based on the relationships and properties encoded in the structured representations.
Diagram 8: Rule Application
2.5.3 Techniques for Symbol Representation
Symbolic AI employs various techniques for representing symbols and their relationships, such as:
Predicate Logic: Predicates are used to represent relationships between objects, such as “isTaller(John, Mary)” to express that John is taller than Mary.
Semantic Networks: Graph-based structures where nodes represent concepts and edges represent relationships between them.
Frames: Data structures that represent stereotypical situations or objects, with slots for relevant properties and their values.
2.5.4 Example Applications of Symbol Manipulation
Symbol manipulation finds application in various AI systems, such as:
Natural Language Processing (NLP): In NLP, symbol manipulation is used to parse and understand human language by representing words, phrases, and grammatical structures as symbols.
Expert Systems: These systems use a knowledge base of symbols representing domain expertise and apply inference rules to provide expert-level decisions or recommendations.
Automated Reasoning: Symbolic AI enables automated reasoning tasks, such as theorem proving, where mathematical objects and their properties are represented as symbols, and logical rules are applied to derive proofs.
2.5.5 Challenges in Symbol Manipulation:
While symbol manipulation is a powerful technique, it also presents certain challenges:
Complexity: As the number of symbols and rules grows, the system can become computationally complex and difficult to manage.
Flexibility: Symbolic AI systems can be rigid and may struggle to adapt to new information or contexts that were not explicitly encoded in the symbols and rules.
Ambiguity and Uncertainty: Real-world data often contains ambiguity and uncertainty, which can be challenging to represent and reason about using strict logical rules.
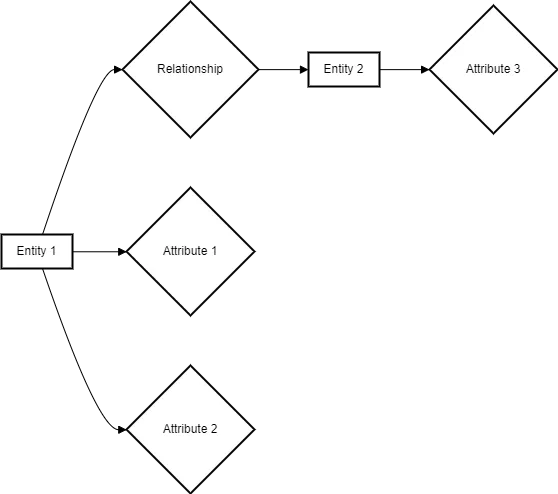
2.6 Ontology:
Ontology is a fundamental concept in Symbolic AI that deals with the formal representation and organization of knowledge about a particular domain. It provides a structured and hierarchical framework for capturing the entities, their properties, and the relationships between them.
In the context of Symbolic AI, an ontology serves as a shared vocabulary and a conceptual model that enables knowledge sharing, reuse, and reasoning. It defines a common understanding of the domain and allows for the integration of knowledge from different sources.
Key components of an ontology include:
Classes: Classes represent the main concepts or categories within the domain. They are organized in a hierarchical structure, with more general classes (superclasses) subsumes more specific classes (subclasses). For example, in an ontology for vehicles, “Vehicle” could be a superclass, with “Car,” “Truck,” and “Motorcycle” as its subclasses.
Instances: Instances, also known as individuals, are specific objects or entities that belong to a particular class. For example, “Toyota Camry” could be an instance of the “Car” class.
Properties: Properties describe the attributes or characteristics of classes and instances. They can be intrinsic properties (e.g., color, weight) or relational properties that define relationships between classes or instances (e.g., “ownedBy” relationship between a vehicle and a person).
Axioms: Axioms are logical statements or constraints that define the rules and relationships within the ontology. They specify the necessary and sufficient conditions for class membership, property restrictions, and domain-specific rules. Axioms allow for reasoning and inference over the ontology.
Diagram 9: Vehicle Ontology
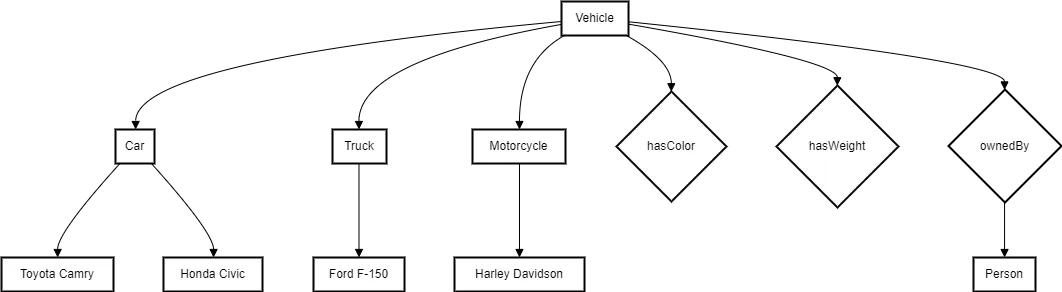
In this example, the ontology represents the domain of vehicles. The “Vehicle” class is the superclass, with “Car,” “Truck,” and “Motorcycle” as its subclasses. “Toyota Camry,” “Honda Civic,” “Ford F-150,” and “Harley Davidson” are instances of their respective classes. The ontology also includes properties such as “hasColor,” “hasWeight,” and “ownedBy,” which describe the attributes and relationships of vehicles.
Ontologies play a crucial role in Symbolic AI by providing a structured and machine-readable representation of domain knowledge. They enable tasks such as knowledge base construction, information retrieval, and reasoning. Ontologies facilitate the development of intelligent systems that can understand and reason about a specific domain, make inferences, and support decision-making processes.
Some popular ontology languages and frameworks used in Symbolic AI include:
-
Web Ontology Language (OWL): OWL is a widely used ontology language that extends the capabilities of the Resource Description Framework (RDF). It provides a rich set of constructs for defining classes, properties, and axioms.
-
RDFS (RDF Schema): RDFS is a vocabulary for describing the structure and semantics of RDF data. It allows for the definition of classes, properties, and hierarchical relationships.
-
DAML+OIL (DARPA Agent Markup Language + Ontology Inference Layer): DAML+OIL is an ontology language that combines the features of DAML and OIL. It provides a more expressive language for defining ontologies compared to RDFS.
Ontologies are widely used in various domains, such as healthcare, e-commerce, and scientific research, to facilitate knowledge representation, sharing, and reasoning. They enable the development of intelligent systems that can understand and process complex domain knowledge, leading to more accurate and efficient problem-solving capabilities.
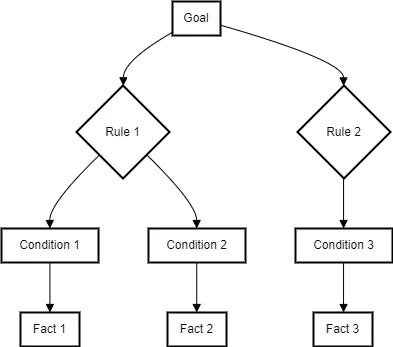
2.7 Inference Engines
An inference engine, also known as a reasoning engine, is a critical component of Symbolic AI systems. It is responsible for deriving new knowledge or conclusions based on the existing knowledge represented in the system. The inference engine applies logical rules and deduction mechanisms to the knowledge base to infer new facts, answer queries, and solve problems.
The primary function of an inference engine is to perform reasoning over the symbolic representations and ontologies defined in the knowledge base. It uses the available facts, rules, and axioms to draw conclusions and generate new information that is not explicitly stated.
There are different types of inference engines used in Symbolic AI, each with its own reasoning strategies and techniques:
Forward Chaining: Forward chaining, also known as data-driven reasoning, starts with the available facts and applies inference rules to derive new facts until a desired conclusion is reached. It works by matching the conditions of the rules against the facts in the knowledge base and firing the rules when the conditions are satisfied. This process continues iteratively until no more rules can be applied or a goal state is achieved.
Diagram 10: Inference Engine (Forward Chaining)

Backward Chaining
Backward chaining, also known as goal-driven reasoning, starts with a desired goal or conclusion and works backward to determine if the goal can be supported by the available facts and rules. It starts by matching the goal against the conclusions of the rules and recursively matches the conditions of the rules against the facts or other rules until the goal is proven or disproven.
Diagram 11: Backward Chaining
2.8 Contrast with Other AI Paradigms
Symbolic AI differs from other AI paradigms, such as machine learning and neural networks, in several key aspects:
-
Symbolic AI relies on explicit, structured representations and logical rules, while machine learning and neural networks learn patterns from data.
-
Symbolic AI systems are typically deterministic and offer clear explanations for their reasoning, whereas machine learning models can be opaque and difficult to interpret.
-
Symbolic AI requires manual encoding of knowledge and rules, while machine learning automatically learns from data, often requiring large datasets and computational resources.
Section 3: Applications and Use Cases
3.1 Expert Systems
Expert systems are one of the most prominent applications of Symbolic AI. These systems aim to capture the knowledge and reasoning processes of human experts in a specific domain and provide expert-level advice or decisions. They use a knowledge base of symbols representing domain concepts and rules that encode the expert’s reasoning strategies.
Use Case: Medical Diagnosis Expert System
A medical diagnosis expert system uses symbols to represent symptoms, diseases, and diagnostic rules. For example, the system may have rules like:
-
IF fever AND cough AND headache THEN influenza
-
IF chest_pain AND shortness_of_breath THEN heart_attack
When a patient’s symptoms are input into the system, it applies these rules to infer the most likely diagnosis based on the symbolic representations and logical inference.
3.2 Natural Language Processing (NLP)
Symbolic AI plays a significant role in natural language processing tasks, such as parsing, semantic analysis, and text understanding. Symbols are used to represent words, phrases, and grammatical structures, enabling the system to process and reason about human language.
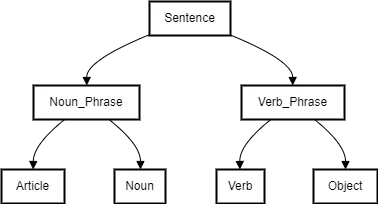
Use Case: Symbolic Parsing in NLP
In symbolic parsing, a grammar is defined using symbolic rules that specify the structure of valid sentences. For example, a simple grammar rule might be:
Sentence → Noun_Phrase Verb_Phrase
The parser uses these symbolic rules to break down a sentence into its constituent parts and create a parse tree representing its syntactic structure.
Diagram 12: Parse Tree
3.3 Automated Reasoning
Symbolic AI is extensively used in automated reasoning tasks, such as theorem proving, logic programming, and constraint satisfaction. Symbols are used to represent logical statements, and inference rules are applied to derive new conclusions or prove mathematical theorems.
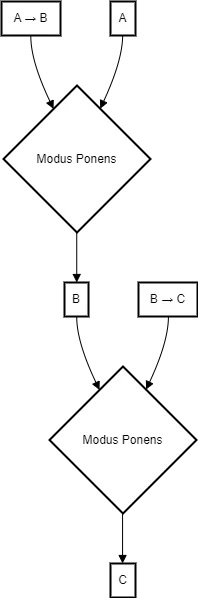
Use Case: Theorem Proving
In theorem proving, mathematical statements and axioms are represented using symbolic logic. The system uses inference rules to construct proofs by deriving new statements from existing ones. For example, given the axioms:
A → B
B → C
The system can use modus ponens inference rule to derive:
A → C
Diagram 13: Theorem Proving
Section 4: Strengths and Limitations
4.1 Strengths of Symbolic AI
Interpretability: Symbolic AI systems provide clear explanations for their reasoning, as the logic and rules are explicitly defined.
Knowledge Representation: Symbolic AI allows for the structured representation of complex knowledge and relationships using logical formalisms.
Reasoning Capabilities: Symbolic AI enables powerful reasoning capabilities, such as deduction, induction, and abduction, based on logical rules and inference mechanisms.
4.2 Limitations of Symbolic AI
Scalability: As the number of symbols and rules grows, Symbolic AI systems can become computationally expensive and difficult to scale.
Brittleness: Symbolic AI systems can be brittle and may fail when faced with situations that deviate from the explicitly defined rules and knowledge.
Knowledge Acquisition: Acquiring and encoding knowledge in a structured form can be a time-consuming and labor-intensive process, requiring domain expertise.
Handling Uncertainty: Symbolic AI struggles with handling uncertainty and ambiguity, as it relies on strict logical rules and deterministic reasoning.
Section 5: Future Directions and Conclusion
5.1 Neuro-Symbolic AI
Neuro-symbolic AI is an emerging approach that aims to combine the strengths of Symbolic AI and neural networks. It seeks to integrate the structured representations and reasoning capabilities of Symbolic AI with the learning and adaptability of neural networks. By leveraging the complementary strengths of both paradigms, neuro-symbolic AI has the potential to create more robust, interpretable, and flexible AI systems.
5.2 Integration with Other AI Techniques
Symbolic AI can be integrated with other AI techniques, such as machine learning, natural language processing, and computer vision, to create hybrid systems that harness the strengths of multiple approaches. For example, a symbolic reasoning module can be combined with a deep learning-based perception module to enable grounded language understanding and reasoning.
5.3 Conclusion
Symbolic AI, with its foundations in formal logic and symbol manipulation, has been a cornerstone of artificial intelligence research since its inception. Despite the challenges it faces, Symbolic AI continues to play a crucial role in various applications, such as expert systems, natural language processing, and automated reasoning.
As AI evolves, the integration of Symbolic AI with other paradigms, like machine learning and neural networks, holds immense promise. Neuro-symbolic AI and hybrid approaches aim to create more robust, interpretable, and adaptable AI systems that can tackle complex real-world problems.
By understanding the foundations, methods, and applications of Symbolic AI, researchers and practitioners can appreciate its strengths, address its limitations, and explore novel ways to harness its potential in the ever-evolving landscape of artificial intelligence.
This primer serves as a comprehensive introduction to Symbolic AI, providing a solid foundation for further exploration and research in this fascinating field.